你在纸上画一条线,你虽然把它当成一维的,但这条线必然是有厚度的,而且必须是对纸张有压迫的,所以必须是三维的。
而且你也必须“看到”了这条线的三维属性,因为如果它是一维的,那么它显然不能挡住从任何方向来的光,那么它显然不可能被看见,如果它是二维的,意味着它没有墨的叠加,它会无限浅,是无色的,所以你能看到这条线,就已经表示这条线是三维的了。
所以既然你看得见这条线,就已经表示了这条线在你的脑中反映了一维空间以外的维度,就表示你的视觉系统并没有把这条线当作“一维物体”来处理。
所以可想而知,你不可能真的想象出一个“一维物体”,因为一个一维物体是根本看不见的。
既然如此,你却依旧觉得你能够想象出“一维物体”,显然是因为你的思维系统把这种画出来的线当成一维处理了。
但你可以把本来是个三维的物体当成了“一维”来处理,为什么就不能把一个本来是三维的物体当成是四维来处理呢?
如果你能把某些本来是三维的物体当作四维来处理的话,你还会问“为什么人类想象不出四维空间”这种话吗?
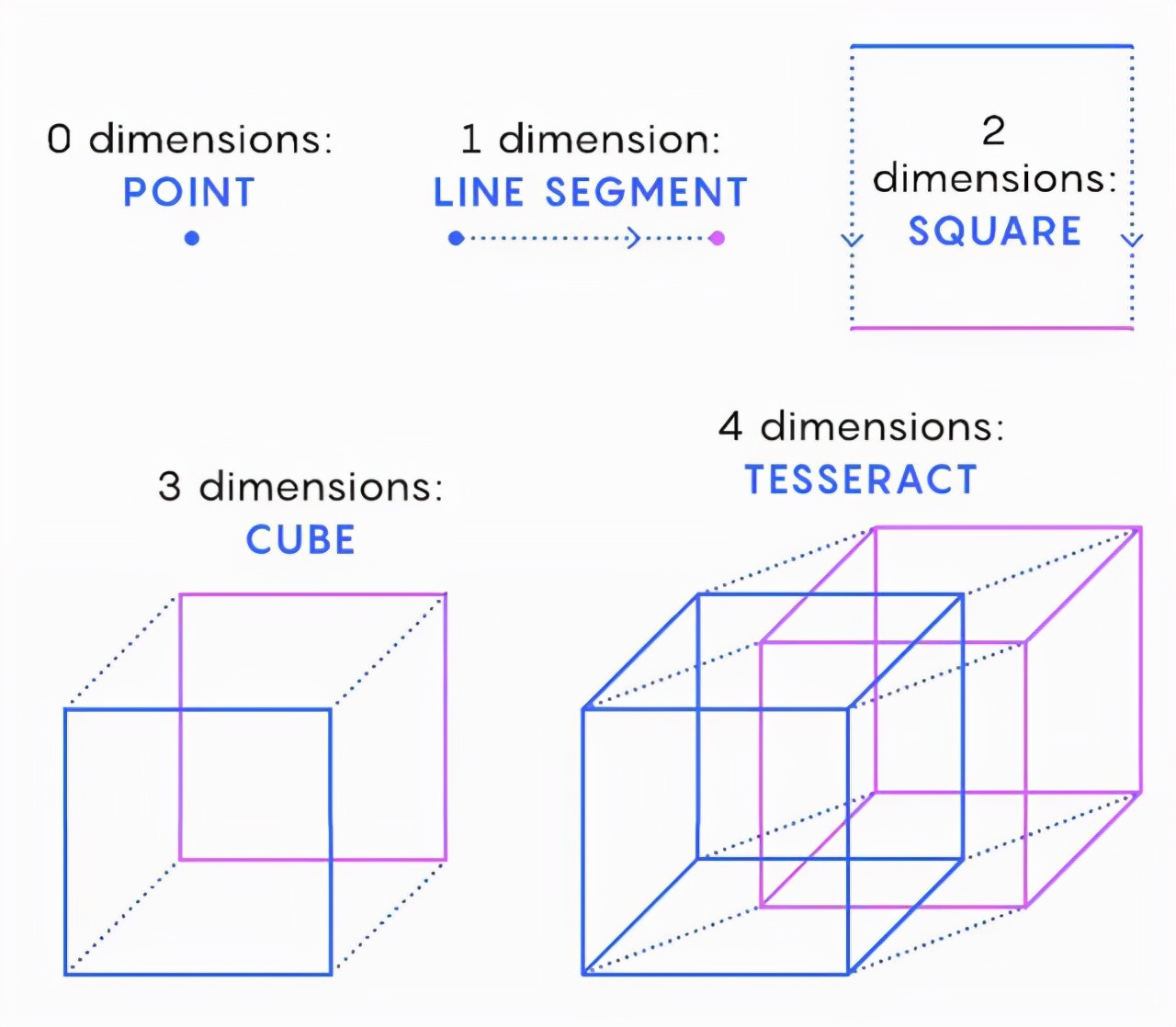
本文的全部内容都是在试图解释,为什么你可以把有些实际上是三维的图形当成一维二维甚至非欧空间的图形进行处理,却无法把三维图形当成四维和另一些非欧空间图形处理的问题,如果我话说到这个份上都还无法理解的话,我实在是无话说了。
很多朋友都有这样的问题:
1:影子是不是二维物体?
2:屏幕里的人物是不是二维物体,
我统一回答一下:
首先这两个问题是相似的,本质上都是指光投影到一个“平面后”是不是二维的。
数学上讲,如果这个平面是“绝对平整”的,那么这必须是个二维的,但现实生活中呢?
现实生活中,并不存在一个绝对“平整”的平面,而且,一个平面的“平整”与否,本身就只有在三维以上的空间中才能确认。
如果有朋友觉得影子或者是纸片人是“二维的”,并以此认为他可以“想象”出来“二维空间”。
实际上,如果脱离了所投影到那个平面,那么“影子”根本就不是一个“物体”,它是一束光达不到的地方,是纯粹的,而且是“三维”的真空区间。
显然如果你真的“想象出来”了一个“二维”的影子,你就必须要“想象”出影子所投影到的那个物体,这个物体既不是生活中常见的“墙”,“地板”或是不那么平整的任何真实存在过的平整物体,而是一个绝对“平整”的平面。
其次,许多朋友都有纸片人老婆,制片人老婆真的是“二维”的吗?
如果这个纸片人老婆在你的脑中真的是“二维”,那么这就必然意味着你老婆的胸和脸在你脑中都是“平”的,试问倘若你真的如此想象你的“老婆”,“她”又是如何吸引到你的呢?
现实生活中,通过相对而言比较“平”的屏幕上的投影,却能让许多朋友产生这种凹凸有致得多的想象,这恰恰说明人脑是本能上“拒绝”想象“绝对平整”的。
所以严格来说你并没有“想象出”二维物体,如我所言,你自以为自己想象出来了,因为你觉得对这些东西而言凭感觉想象一个第三维也无所谓。
到这里,又有朋友问,为什么我要求必须是“平整”的,这段话你们之后补充完知识再看。
如果你们默认空间中的距离是欧式距离,那么二维的曲面就只能在三维以上空间中定义,如果你不想像第三个维度的话,你怎么能知道这个二维面是“曲”的呢?

一张纸不管它怎么弯曲,它投影到任何一个“平面”上都是“二维”的,都是平的,要反映这张纸是“弯曲”的,你只能放在三维空间中想象。
如果你要在二维空间以内就认识到这个曲面是曲的,那么你必须更改这个曲面内“距离”的定义,在这个“距离下”,三角形内角和不一定是180度,两点之间未必直线最短,圆周率不一定是3.14159···,如果你改了“距离”的定义,那么这就不再是一个欧几里得空间了,甚至连“维度”的定义都会改变,我们首先得认为题主的“四维空间”必须指的是四维欧式空间,否则还真的无法讨论。
如果我们把“想象出具体形状”的这个要求剔除出去,仅仅只要求理解空间的性质的话,人类不仅能够想象出四维空间,还有各种各样的空间。
而如果我们非要把“想象出具体形状”定义为“想象”的话,那么就的确做不到了。
一,首先我先补充一下关于“空间”的知识。
在数学上,拓补空间是由开集合构成的集合族,也就是说你随便找一群符合条件的集合,其实都可以构成空间。
一切几何问题,本质上都是点与点的距离问题,如果我们试图从度量点的坐标和距离来认识和“想象”空间的话,“度量空间”的定义和“距离”的定义就往往是一起的,也就是说,空间究竟是什么样的,取决于你对两点间“距离”的认识。
两点的“距离”的定义是需要满足三个条件的实数,这三个条件是。
1:非负同一性:任何两点的距离都必须大于等于零,每一个点到它自己、且仅到它自己的时候,距离等于零。
2:对称性:点A到B的距离必须和B到A的距离相等。
3:三角不等式,A到B的距离与B到C的距离之和,必须大于等于A到C的距离。
一旦点与点的“距离”关系被给定了,那么空间所具有的性质,和空间中点与点之间的关系就被给定了,也可以说这个空间的“形状”被给定了。
有一种特殊的“距离”,还满足第四个条件:
把A的坐标乘上一个常数a得到点aA,如果点aA到原点的距离刚好是A到原点的距离的a倍,即距离和坐标满足线性关系,那么就把这个“距离”叫做“范”(norm),这个空间被称作赋范空间。
现在,我们很清楚了,日常生活中,两点的距离是等于根号下两点各个坐标差的平方的和的,我们称这个距离为欧式距离,这个空间为“欧几里得空间”。
显然,欧式距离是一种“范”,欧几里得空间是一种“赋范空间”。
二,“想象不出”的空间多了去了。
现在你恐怕已经知道各种空间的情况是有多复杂了吧?
我再随便给你一个范:
曼哈顿距离,
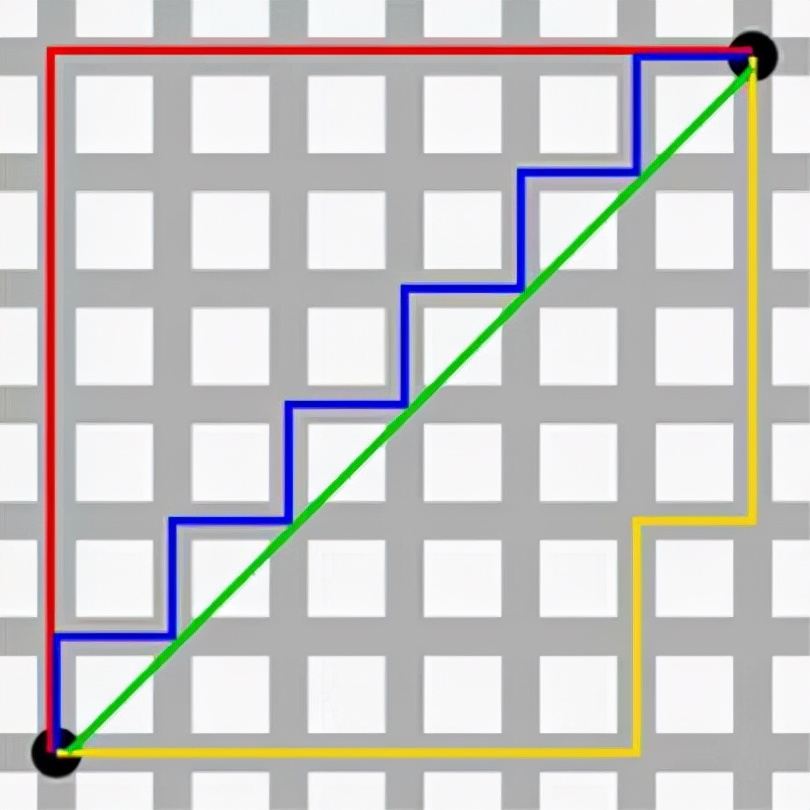
曼哈顿距离指的是两点之间各坐标差的绝对值的和,即对于A(x1,y1),B(x2,y2)两点的距离,如果被定义为| x1-x2 |+|y1-y2 |的话,那么这个距离就被称为曼哈顿距离,图中绿色的线表示的就是两点间的欧式距离,而图中红黄蓝三线都可以表示两点间的曼哈顿距离。
其实这就如同你在曼哈顿开车,不能直接穿过一幢幢大楼,而只能拐弯是一样的。
上图看上去曼哈顿距离姑且还可以被放在“欧式空间”中进行“想象”,实际上,这和我们这些三维空间生物想象出二维空间并无什么区别。
然而当两个点距离取得无限小的时候,就相当于有无限个无限小的楼房卡住了路中间,任何两个有一个坐标不同的点之间都无法用一条“像是欧式空间的直线”连接起来,即使他们无限逼近。也只能不断使用折线来连接这些点。
如果你非要去想象这无数个无限小的楼房卡住了位置来帮助你“理解”这个距离的话,你也是做不到的。
正如你如果非要去想象一个“无穷薄”的物体来“彻底”理解“二维空间”,你也是做不到的。因而你之所以觉得你“想出了二维空间或者曼哈顿空间”并非是因为你真的“想象出”了无穷薄的物体或者无穷多个无穷小的小房子,而是因为你觉得想不出这些也无所谓。
那么我再给你个空间:
距离d(x,y)=1,如果点x不等于点y
距离d(x,y)=0,如果点x等于点y。
这个距离显然满足“距离”的三个条件,非负同一性,对称性,和三角不等式,但它显然不是一个范。
如果你非要用脑子去想象这个空间的形状,那么你只能想象到4个点,它们如果非要用欧几里得空间的点来表述,刚好在欧式空间中形成一个正四面体。
这种空间别说想象出几维,甚至连“维度”都难以定义,你非用脑子想其实就是自讨苦吃。
可见,在数学上可以写出来,但你却“想像不出”的空间多了去了,远不止四维的或是高维的欧几里得空间结构。
接下来我们回到一开始的问题上,为什么你能把一些三维图形当成二维或是一维的图形处理,而却不能把一些三维图形当成四维空间处理?
许多朋友可能会得出一种简单的归纳———那就是高维空间不能被人脑当成低维空间的图形来处理,这种归纳对不对呢?的确不错,但这种归纳是远不够深入的,正如我前面所补充的知识,空间的种类是无穷的,远不止四维的欧式空间,甚至有一些空间,你都不能定义维度,那么哪些空间是可以三维图形所处理的,你用欧式空间的维度的高低的概念来回答这个问题是很不完备的。
于是我展开了下面的分析。
三:“想象”究竟是怎样一个过程?
(数学家们并不关心人类的“想象”究竟是什么,所以我这里只能自行分析,如有不对还请指教。)
讲到这里,你恐怕就已经懂了,人不过是一种三维欧几里得空间的生物,所谓“想象”,其实就是把一个空间中所有点集都对应到三维的欧几里得空间中而已。
显然,如果一个空间中的所有点都能“轻易”对应到三维欧式空间中,你便会觉得你想象得出来。
那么这个“轻易”又指的是什么?
就我目前的想法而言,我认为如果这个对应可以是一个“单射”,而且可以是一个可以微分的对应,那么就形成了“轻易”,你就会觉得你自己把整个空间“想象”了出来。
比方说,尽管你并不能去“想象出”无穷薄的纸或者无穷个无穷小的楼房,但你依旧觉得“自己想象”出了“二维空间”或是“曼哈顿度量空间”。
为什么呢?
因为你觉得自己想象不出来无穷小的厚度或是无穷小的楼房这些东西也无所谓,因为你随便想一张纸,便觉得你的“想象图形”保留了原来这些点的全部性质,也就是说这是因为最起码的,原来图形的每一个不同的点,在你“想象”的新的图形——那张纸中都可以找到不同的点来对应。
换言之,你的“想象得出与否”的标准,其实就是看你能不能建立一种单射(我稍后会强调可微的属性),使得你要想像的那个空间中的点能够对应到三维欧式空间中。
(单射,是指这样一种对应:
对于集合A中的每个元素,集合B都最多有一个元素与之对应,且集合A中任何两个不同的元素,在集合B中有对应的话,都一定对应两个不同的元素。)
显然,二维欧几里得空间中的任何点构成的点集(x1,y1),(x2,y2),(x3,y3)···随便加上一组坐标变成,(x1,y1,z1),(x2,y2,z2),(x3,y3,z3),这就构成了一个单射,如果把z坐标设置为恒为零。
f(x,y)—— x,y,0,很显然,这是一个可微的单射。
你平时“想象”二维空间的物体,比如说一张平坦的纸,其实就是你直接把二维空间的点集的第三个坐标默认为了一个常值,马上就能得到一个连续可微的单射对应。
实际上,如果在z坐标上做手脚,变成一些复杂的对应,许多朋友的“想象力”就很难跟上了。
比如想象一张倾斜的,弯曲成各种形状的纸,就比想象一张平整的纸难得多,而究其根源,就是这个对应的复杂程度变高了嘛。
而当这个对应到了无穷“复杂”,人类的想象力自然也就无法跟上了。
你想像不出四维欧式空间,也许就是因为把四维空间中的点集对应成三维欧式空间中的点集的可微单射不存在的原因。
比如说,四维空间中的点(x,y,z,w),如果你拿掉w坐标。
即构成映射f(x,y,z,w)=(x,y,z),这样就对应到三维空间中了。
这个映射显然不是单射,因为(x,y,z,1),和(x,y,z,2)会对应到同一个点(x,y,z)。
如果你去“想象”这样一种不是单射的对应,显然你会觉得自己没有充分的“想象”出四维空间中点的分布,因为自己认为把本来的许多个点,比如(x,y,z,1)和(x,y,z,2)对应成了一个点,因此你不会觉得自己“想象出”了四维空间。
所以如果不是建立起一种“单射”对应的话,你不会觉得自己把它“想象了”出来。
但熟知集合论的朋友也知道,其实你可以找到四维空间到三维空间的一种单射,因为不管n是几,n维空间中点的数量都是阿列夫1。
比如说,按照康托尔坐标划分的方法,其实四维空间可以建立起到三维空间的这样一种单射,
f(x,y,z,w)——f(x,y,b)
其中,b是z和w结合的一种构造,比如原来的z=100,w=234,b可以设置成奇数位是z的数字,偶数位是a的数字的坐标——120304。
这样,你把坐标z和a任取两个实数,比如说z=123,w=456,就可以得到一个独一无二的b,142536,而且显而易见这样一个对应中只要z和a任何一个发生变化,b就必然和原来不同。
因此z,w——b就构成了一个单射,但显而易见,这个单射如我所言,不是可微的,它甚至都不是连续的。
关于“可微”的定义,我就不多说了,学过微积分的都懂,但是这里强调一下,欧式空间中连续和可微用的是欧式距离来定义的,(就是说两初始点点距离无限接近的时候,两个对应点的距离也无限小且二者比例是在任意方向上都是有界的定值,这里也是一样,对应点之间的距离用欧式距离,只不过初始点之间的距离用那个空间定义的距离而已。)
我在这里强调一个“可微”的概念,是因为我即使你用一个单射把点和线对应成体和球,人类的脑子也不可能同时想象出无限个球,除非这些球连成了一个形状,且构成了一条有限次“均匀”变化的形状,人类所能“想象出的”不是离散物体的形状,无非都是有限个“均匀变化线”的组合,而如果不谈“线性”,只谈点的话,其实是无法构成“维度”的。
因此四维空间中的任何一条连续的均匀变化线,因为其本身含有无穷个点,所以都在只有被对应成三维空间中一条“有限个均匀变化的组合”的时候,才能说人类“想象了”出来。
所以我强调这必须是一个有限个可微对应组成的单射,因为我认为,人的脑子不能“想象出”无限个离散的物体或者无限次不均匀的变化,因此将四维空间中的一个超平面对应成三维空间中无穷个离散体或是不均匀变化的方法并不能帮助人类进行这种“想象”,实际上,这是把人脑处理的“对应的复杂程度”提高到了无穷大,所以如果不是一种可微对应,那么人脑就无法运作了。
四,我关于“想象”的分析的佐证
关于这种“想象不出”的事情,在历史上曾经发生过一次。
1872年的时候,韦尔斯特拉斯在论文中曾经给出了一个非常有名的函数,这个函数被称作韦尔斯特拉斯函数。
在这个函数被提出之前,所有数学家都没有想到“一个处处连续,但处处不可微”的函数。
在早期数学家的直觉和“想象”里,这样的函数是不存在的,他们直觉上认为,即使对于任何一个不可微的连续函数,你只要分割到足够小,那么也会是可微的。
我提到过,这之所以违反直觉,是因为人类的脑子根本无法“想象出”一个在有限空间里能无限次不均匀地变化的形状,如果人类的脑子真的能想象出无限次的“不均匀变化”,那么用纯粹的数学解析式以外的方法预料到“韦尔斯特拉斯函数”的出现是理所当然的。
直到今天,人类别说是四维空间,就是韦尔斯特拉斯函数的形状,都无法充分地“想象”出来。
所以如我所言,要让人类“想象出”四维空间是不可能的原因,很可能是因为四维空间到三维空间无法建立起一种可微单射所导致的。
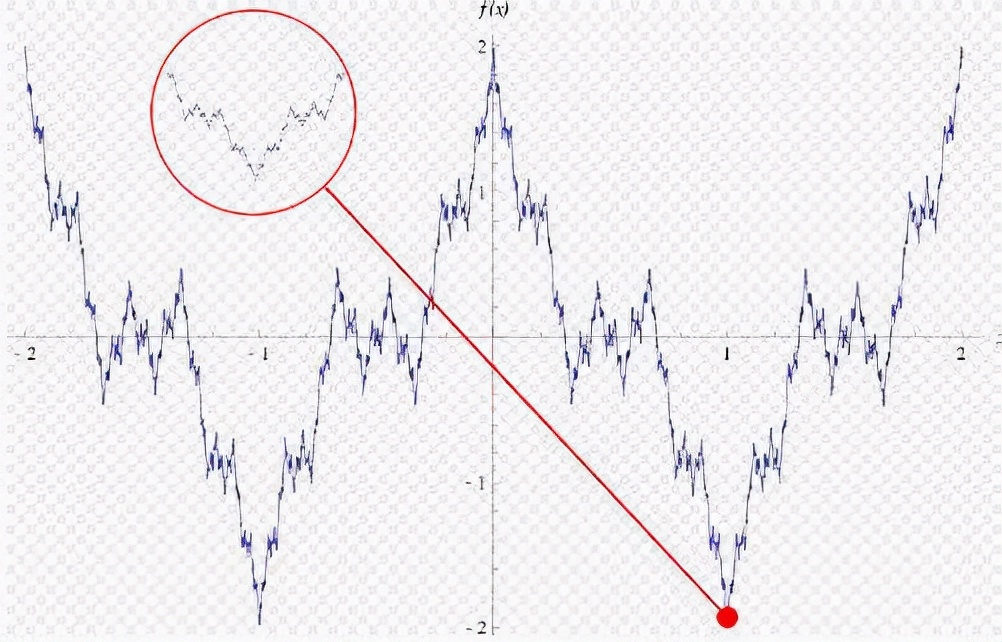
看上去像是有意义的韦尔斯特拉斯函数的画法
当然关于“想象”这个事情我也不能下出完全的论断,毕竟没人能说明“想象”究竟是什么,如果有数学大神觉得我的思考出现了问题也可以指出我的错误。
此处我要强调的是,空间的种类有无数种,而欧式空间只是其中之一,三维以下的空间又只是欧式空间的一小部分,你甚至都不能能“觉得自己想象出”我给出的那个空间的第五个点,而且你就连二维空间中的形状也未见得总能“自以为想象得出”,比如韦尔斯特拉斯函数。
因此,人类的想象力,虽然是无穷的,但也是匮乏的。
如何理解人的想象力既无穷又匮乏呢?就如这阿列夫零,虽然是无穷的,但相对于阿列夫一,就是“匮乏”的了。
而想象出四维欧式空间其实根本就不重要,数学家们不仅不能想象出四维空间,也不能想象出各种拓补空间,但这丝毫不影响他们研究这些空间中的几何学。


